Information goods have negligible marginal costs, and this will create possibilities for novel distribution and pricing methods. The main concern of this paper is with pricing of goods that are likely to be consumed in large quantities by individuals. For example, will software continue to be sold at a fixed price for each unit, or will it be paid for on the basis of usage? There is substantial evidence both from observing marketplace evolution and from surveys that customers overwhelmingly prefer subscription pricing. It turns out that even if we ignore this factor, per-use pricing is not a clear winner, and therefore when the preference effect is taken into account, subscription pricing is likely to dominate.

We model competitive pricing between two companies that supply essentially equivalent services (such as movies or word processing software). One company charges a fixed fee per unit, while the other charges on a per-use basis. Each is interested in maximizing its revenue. We consider instances of the models that have stable competitive equilibria between suppliers along with situations that are unstable and, in the absence of collusion, lead to ruinous price wars.

Contents

Introduction
Consumer and producer preferences in pricing plans
Optimal pricing for a monopolist
Fixed-fee vs. pay-per-use competition
Dynamic behavior, equilibria, and price wars
References

Introduction

There are wide expectations that electronic commerce, especially in "soft" or "information" goods (such as news stories, software, network games, database access, and entertainment) will move largely to à la carte pricing. Consumers will select the items they want, and pay for each through one of the many micropayment schemes that are being developed. However, economic arguments and observations of market behavior show that this is unlikely to be the dominant mode of pricing for established producers Odlyzko (1996), Varian (a) and Varian (b). Information goods are characterized by negligible marginal costs, and therefore arguments in favor of bundling are stronger for them than for physical goods. The combination of matrimonial ads and reports of boxing matches that appears in print newspapers might appear to be caused by the impracticality of producing physically separate editions for each one. However, bundling arguments show that producers can obtain more revenue by combining disparate items, since that allows them to exploit uneven preferences that consumers have for different goods. While it is not true that bundling is always better than offering items separately, in most situations bundling is advantageous to the producers, since it depends only on moderate variations in preferences Bakos and Brynjolfsson (1997) and Schmalensee (1982) (see also Odlyzko (1996) for various examples). Hence in the future we are likely to subscribe to electronic newspapers that carry wide ranges of stories (even though the selection of those stories might be personalized), and not buy individual stories.

The arguments in favor of bundling are strong, and suggest that à la carte or unit pricing will not be the dominant mode of commerce in information goods. However, unit pricing is still likely to be widespread. For many goods, that appears to be the most appropriate approach. Moreover, even if bundling does dominate, as we predict, there are likely to be niches for fixed-fee sales. Newspapers probably will be selling individual stories. All we suggest is that they will contribute a small part of total revenues, just as is true today. One of the few general results about the economics of bundling is the observation of Adams and Yellen (1976) that mixed bundling (in which items are offered for sale separately, as well as in combination, but with the price of the individual items higher than they would be otherwise) is always better (with proper prices) than pure bundling, in which items are available only in combination. Hence we might see the electronic version of the New York Times available through annual subscription for $0.50 per day, a single day's edition for $1.00, and individual stories for $0.25, say. Furthermore, bundling is most appropriate for producers with an established brand. An amateur selling Christmas card designs is most likely to sell them à la carte. The many frustrated authors, who feel they are not getting into print because of a conspiracy or stupidity of publishers, are likely to attempt selling their works themselves. Even though most of them are likely to be disappointed by the outcome, this will create demand for micropayment systems. (Furthermore, there will be enough successes to keep up the interest. After all, shareware revenues do provide comfortable living for many programmers, even though shareware is a small factor in the entire software industry.)

Chuang and Sirbu (1977) argue that publishers will benefit from a combination of unbundled and bundled sales of scholarly journal articles. Since the majority of scholarly journals are purchased by academic libraries and not individuals, and this market is both unstable and full of perverse economic incentives not easily captured by standard economic models (see Odlyzko (1997) for a discussion of this subject), we feel that the Chuang and Sirbu analysis is most appropriate for publications aimed at individuals. Further, even in those cases, the consumer preferences discussed in Section 2, which are hard to take into account in the conventional economic utility maximization model of Chuang and Sirbu (1977), suggest that the balance will be tilted more towards subscription pricing than individual article sales.

Most of the discussion of the advantages of bundling in Bakos and Brynjolfsson (1997) and Odlyzko (1996), for example, was about one-time sales of several different items, and the arguments were that bundling is likely to be advantageous to the producers in most cases. In this paper we consider à la carte versus prix fixe approaches to sales of many units of the same or similar good, for example software or entertainment programs. While most of the sales to consumers are on the fixed price (for software) or subscription (for cable TV, for example) basis, there is frequent discussion of per-use pricing. The entertainment industry continues to test such schemes. One of the big attractions of Java, downloadable applets, and the Network Computer to the software industry seems to be the possibility of charging consumers according to their usage of a particular product. There is a widespread feeling that selling shrink-wrapped software allows heavy users to avoid paying a "fair share" of the development cost. Moreover, even some consumers speak up in favor of per-use pricing. There are many people who do not use Microsoft Word often, but when they do need to use it, they have an urgent need to do so, typically to read documents prepared in that system that are sent to them. These people find it worthwhile to buy (or have their employer buy) the latest version of Word for just such use, and would benefit from per-use pricing. (See, for example, the discussion in Picarille (1996).)

While there are obvious attractions to per-use pricing, the basic economic arguments based on utility theory are not as clear as for bundling, where those arguments strongly support the idea of selling combinations of items. Producers would (in the absence of competitive alternatives) gather more revenue from heavy users, but less from the light users. For some distributions of demands, per-use pricing might be more advantageous than fixed-fee plans. However, in Section 3, we present some computations that show that if consumers attach well-defined values to information goods, and know how much of each good they are likely to consume, a monopolist can, for many reasonable distributions of values, obtain more revenue from a fixed-fee pricing plan.

While the simple utility maximization argument might favor per-user pricing in a substantial fraction of cases, what we observe in the market are repeated failures of à la carte pricing. Many pay-per-view TV schemes have flopped. Furthermore, there has been a tremendous pressure from consumers towards subscription plans for information services. The flat-rate Internet access plan may not be viable, since there are substantial marginal costs in providing such services, but the strong consumer preference that has forced even America Online to switch to fixed-fee pricing has to be taken into account. In Section 2 we discuss some of the extensive evidence that is available in the literature for this preference, and the reasons for it. This preference is not easy to take into account in standard economic models (other than by saying, as Baumol reportedly did, that consumers derive a positive utility from prix fixe pricing), but it appears to be a major factor that will favor fixed-fee schemes, at least for individual consumers. (For businesses, the evidence from market behavior is that they are more willing to accept per-use plans than are consumers.) Content producers can take advantage of this preference by charging higher prices than they would if consumers behaved more as utility maximizers. In Section 2 we also discuss other arguments, which are again not easy to cast into quantitative economic terms, as to why even producers might favor flat-rate plans.

While producers of information goods typically have a monopoly on their product (after all, there is only one New York Times, and in general copyright laws provide protection for the producers), this monopoly is seldom perfect. Readers of the New York Times can switch to the Washington Post, or rely on online access to Associated Press dispatches, say. Competition is always present, even in muted form, and constrains pricing decisions, including the extent of bundling. Unfortunately it is hard to model competition in information goods. If two producers offer the same good with zero marginal costs for distribution of an additional unit, then each producer can undercut the other one, if only by a small margin, and gain revenue and thus profit. Since the other producer has the same incentive, in the absence of collusion, the only possibility is for a ruinous price war that drives prices to zero. To have a realistic model, we would need to include product differentiation, customer inertia, network externalities, and product evolution, all at the same time. Since we cannot do that, we study some much simpler models in Section 4, in which one producer offers its product on a per-use basis, and the other a competing and nearly equivalent product on a fixed-fee plan. We do not put in any bias towards subscription pricing into our model, and assume that consumers know their usage and choose the cheaper of the two options. We find that in most cases, in the absence of collusion, there is destructive price competition. In those cases where we find a competitive equilibrium, it typically favors the producers charging on a fixed-fee basis. Furthermore, the competitive equilibria we do find yield much less revenue for the content producers than a monopolist could extract.

What conclusions can we draw from our observations? The models in Section 4 show that the simple utility maximization argument does not lead to a clear win for per-use pricing, and (as discussed in Section 2) consumers are willing to pay a lot to avoid it. It seems likely, therefore, that subscription or fixed-fee approaches are likely to continue to be more successful in selling software or entertainment goods than per-use schemes. We do not exclude the possibility of various sliding-scale plans (with a charge for each use that declines with the quantity used), but strongly suspect that pure à la carte pricing schemes will not be successful in the marketplace.

Consumer and producer preferences in pricing plans

There is considerable evidence of consumer preferences for subscription over per-use pricing. Much of it is anecdotal, but there are quantitative measures of just how much extra people are willing to pay for fixed-rate plans. Many of the examples come from telephone service experiments. For example, during the 1970s, the Bell System started offering customers a choice between the the traditional flat rate option, which might cost $7.50 per month, and allow unlimited local calling, and of a measured rate option, which might cost $5.00 per month, allow for 50 calls at no extra charge, and then cost $0.05 per call. Anyone making fewer than 100 local calls per month would be better off with the measured rate option. However, in the numerous trials that were carried out, the flat rate option was usually selected by over 50% of the customers who were making fewer local calls than the 50 covered by the measured rate basic charge, even though they clearly would have benefited from per-use pricing. These results are documented in Cosgrove and Linhart (1979), Garfinkel and Linhart (1979) and Garfinkel and Linhart (1980). Similar preference for subscription pricing was observed in the choices made by customers signing up for various AT&T long-distance calling plans in the 1980s, in which many people paid for plans that provided more calling than they actually used Mitchell and Vogelsang (1991). More recently, this same observation was made about a flat-rate calling plan offered by SBC in the Rio Grande area Palmeri (1996). In the online service area, it has also been common for customers to pay for larger blocks of time than they used.

There are three main reasons that probably lead consumers to prefer flat-rate pricing, and they were recognized a long time ago Cosgrave and Linhart (1979), Garfinkel and Linhart (1979) and Garfinkel and Linhart (1980): (i) Insurance: It provides protection against sudden large bills. (What happens if my son comes back from college,and starts talking to his girl friend around the clock?) (ii) Overestimate of usage: Customers typically overestimate how much they use a service, with the ratio of their estimate to actual usage following a log-normal distribution. (iii) Hassle factor: In a per-use situation, consumers keep worrying whether each call is worth the money it costs, and it has been observed that their usage goes down Garfinkel Garfinkel and Linhart (1980). A flat-rate plan allows them not to worry as to whether that call to their in-laws is really worth $0.05 per minute.

All three factors are part of a general preference by consumers for simple and predictable pricing.

In addition to the consumer preference for flat-rate pricing, there are reasons for producers, especially in areas like software, where network externalities are important, to also like these plans. Since per-use pricing does repress usage Garfinkel and Linhart (1980), it goes counter to the producer's desire that a software package be used as much as possible in order to lock customers into that product. Producers would like consumers to become so used to the particular features and commands of their software that they will find it hard to change to another system. Producers also want their systems to be easy to try out, and be widely used, to capture additional customers. Subscription pricing and site licensing promote these goals.

In general, subscription plans also make it easier to develop close relations with customers. If access is on a strict per-use basis, there is no reason to obtain information about the users. On the other hand, subscription pricing lends itself to finding out what the consumers need, and to customization of offerings.

Optimal pricing for a monopolist

In this section we argue that a flat fee is better than a metered rate for a monopolist selling information goods on the Internet. We give an example to indicate that in the market of information goods, coexisting companies must differentiate themselves more than in a market with distribution costs.

We restrict our price and demand curves to simplify the monopolist's problem of optimizing profit. The restriction on demand curves implies the restriction on price curves -- a company serving consumers represented by our demand curves will optimally set a price curve of restricted type. The restrictions on price and demand curves together imply that each consumer finds it optimal to watch only the price of one quantity, rather than the whole price curve. As some examples show, the monopolist may earn more from a flat fee or from a metered rate, depending on the distribution of consumers; we feel that the population distributions for which a flat fee is most profitable are more natural than the other populations. This contrasts with the situation in many real world markets, in which a high distribution cost makes the metered rate more profitable. Our restrictions about price curves extend nicely to competitive models: a consumer of our restricted type, when faced with multiple companies offering price curves of our restricted type, still shops simply, making his decisions based on the price at only one quantity rather than the whole curve. So some competitive situations are amenable to our simple analysis as well. We find that the Internet market requires companies to differentiate their products more than do markets with distribution costs. Similar companies can coexist normally if they face a distribution cost, and their price curves are constrained so that they must split the market: one company may offer better deals on bulk service, while the other is optimal for consumers buying small quantities. Without the distribution cost, the companies must enter a ruinous price war.

It simplifies our computations if each consumer chooses what quantity of service to buy (or not buy) before examining the available prices. The monopolist serving such rigid consumers can set the price of each quantity of service independently. If no consumer shopping for small quantities would consider buying bulk, then the monopolist can disregard the price of bulk service when setting the price of a small quantity. We want to simplify the monopolist's problem this way. Under what restrictions on price and demand curves is this consumer behavior reasonable? If the consumers have a constant demand for services up to quantity q (and no demand for more), then the optimal price is increasing, and has decreasing unit price. The conditions of increasing price and decreasing unit price imply the price curve is continuous.) That the price increase and unit price decrease, and the demand be constant and positive, and then 0, is sufficient to insure that each consumer maximizes utility by buying either nothing or everything he has a positive demand for.

Our simple structure for consumers' demands allows a two-dimensional parametrization. Each consumer has demand d for up to quantity q of service; the maximum this consumer will pay is w = qd. It is convenient to view the consumers in the q,w plane because price curves and willingness to pay curves (the integral of the demand curve) are functions from q to w. If the consumers' density in the plane is (q,w), then (independently for each q) the monopolist sets the price p(q) to maximize p(q) times the population willing to pay more than p(q) for quantity q. If at some q the consumers are uniformly distributed over some interval of w-values, the optimal price is half of the maximal w among consumers or the minimal w among consumers, whichever is larger. This reasoning, applied at every q, determines the monopolist's best price when faced with a population uniform in the area between two functions from q to w. To assure that the resulting price function has diminishing unit price, we could assume that the functions bounding the population of consumers have. Or let the population as a function of w be independent of q, but scaled by Let be that p maximizing Then our monopolist's optimal price is

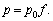
In the q,w plane, we can see the price function p(q) = w and the distribution of consumers simultaneously: those with w values below the price function buy no service; those above buy their preferred amount. If is uniform on a rectangle containing the origin, then the flat fee is optimal and earns 33% more than the metered rate. But there are two other parameter spaces: q,d and d,w, where is the consumer's demand. A uniform population on the same rectangle is in d,w space favors the metered rate by 47%. Finally, a rectangle is in q,d = q,w/q-space is equivalent to a population in q,w-space which is independent of q but for a scaling factor which is a constant multiple of q. By the last sentence of the preceding paragraph, a metered rate is optimal for this population. So for a uniform population on a rectangle containing the origin in either of our alternate parametrizations the metered rate is better. Why? The population distribution has three parameters: q,w,d. A uniform rectangle (containing the origin) in two parameters hides a very wide distribution in the third parameter. Apparently, wide distribution in d, with the other two parameters constrained, favors a flat fee. But if the distribution is widest in one of the other two parameters, then the metered rate is better. Which, in reality, is most likely to vary widely? For information goods, d may well have the greatest variation, and a uniform distribution would approximate (q,w) better than it approximates (q,d) or (d,w). For noninformation goods, one of the other parameter spaces may be more reasonable. For non-Internet markets, the cost of distribution may also make the metered rate more attractive. Indeed, the cost of distribution may be simply passed on to the consumers, so that the price of various quantities is the profit plus the linear, or metered, distribution cost.

Distribution cost allows companies to coexist which sell similar or even identical services. If they are free to set arbitrary price curves, then each can subtly undercut the other, and a price war is inevitable. So we restrict the price curves to be piecewise linear, with some fixed number of pieces. In the presence of a distribution cost, this allows many companies to coexist, each reaping the same profit, so that neither is tempted to trade the other's price curve for his own. But if there is no distribution cost, then the companies must fight a price war. No company alone found it optimal to set a price schedule which would entice a user to buy any other quantity than his entire desired quantity of service, or nothing. Each price curve is increasing, with decreasing unit price. So the minimum over any collection of price curves is also increasing, with decreasing unit price. Equivalent to the condition that unit price decrease is the condition that any ray from any point below the origin on the w-axis intersects the price function only once; clearly this property is preserved under taking the minimum of functions with this property. So each user buys his total desired quantity or nothing at all. Given a collection of price functions, each of which is the minimum of them all at some point, we can introduce a distribution cost which is only slightly less than the minimum of the price functions, so that whichever company lowers its prices to pick up some new consumers begins to serve consumers which are a liability to serve. If we alter the population of consumers, we can create very many of these consumers no one wants to serve. Then we can place profit-yielding consumers barely above the minimal price function, and vary their density with respect to q so that the profit to the various companies is equal. So for any collection of price functions, each of which is somewhere the minimum of them all, there exists a population density and a distribution cost making that collection of price functions a competitive equilibrium. Without any distribution cost, however, each company finds it optimal to undercut one of its neighbors by lengthening or lowering one of the pieces of its piecewise linear price curve. So there is no competitive equilibrium.

Fixed-fee vs. pay-per-use competition

We use two models with somewhat different emphases to examine analytically competitive pricing between two companies, denoted by A and B. Company A charges a fixed subscription fee per unit, for example $20 per month, whereas B charges on a per-use basis, for example $1 for each use or hit. We denote A's fee by a, and B's per-use cost by b. It is assumed that a and b are fixed within each time period, whose length equals the time unit for A's fixed fee, but the companies can change their fees from period to period. Such changes are announced prior to the beginning of each new period. At that time, every customer decides whether to use A or B or neither in the next period. Thus, over a succession of periods, an individual customer might choose A, then A, then B, then neither, then B, ….

The models presume characteristics for the population of potential consumers that remain unchanged over time. When a and b are announced for the next time period, every customer chooses A or B or neither for that period on the basis of a straightforward minimum cost calculation according to the particular aspects of the model. Given these choices, we denote by A(a,b) the average revenue per consumer paid to A, and by B(a,b) the average revenue per consumer paid to B. Thus, if there are N potential customers of the service, A earns NA(a,b) and B earns NB(a,b) during the period in which a and b are in effect.

We now describe the two models. In both, a and b are treated as continuous variables for analytical convenience. We assume also that other parameters, such as customer usage rate and willingness to pay, are continuous, and that probability functions or probability density functions defined for these parameters are continuous and differentiable.

Model 1

Let x denote the expected number of hits per period for a potential customer if the customer actually uses the service provided by A and B. We assume that x has a probability density function over the population of potential customers, with . The probability that a customer chosen at random has ,] is assuming of course that

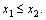
An additional probability overlay for single-customer variability will be avoided by assuming that a customer's expected usage x is its actual usage if it subscribes to the service. We refer to x as the usage rate of a potential customer. This usage rate remains constant over time for each customer. If a customer with usage rate x subscribes, it pays a during the period if it uses company A, and pays bx if it uses company B. Thus, assuming that customers are cost minimizers, a customer with usage rate x

pays a to A if a bx, or

pays bx to B if bx < a,

given that it uses the service.

Model 1 incorporates a notion of willingness to pay by assuming that there is a probability function P on t 0 such that P(t) is the probability that a customer will actually use the service when it would pay t if it does so. Thus, a customer with usage rate x will subscribe to the service with probability

and will not subscribe, hence pay nothing to either A or B, with probability We have for all t, and anticipate that P decreases in t, i.e., that probability of subscribing decreases as the cost of doing so increases. It should be noted that P is defined independently of x. This may be unrealistic in settings where we expect heavy-usage customers to be willing to pay more. We use this feature in our other model.

It follows from our definitions and assumptions for Model 1 that the average revenues per consumer to A and B for a period in which (a,b) applies are

(1)

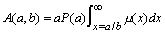
(2)

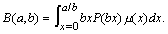
Under the assumption that the companies know and P, we are interested in their choices of the cost variable under their control -- a for A, b for B -- when they desire to maximize their own revenues. We return to this after we describe the second model.

Model 2

Model 1 is an all-or-nothing model which says that a potential customer with usage rate x either does not use the service at all or subscribes and uses it x times during the period. This may be appropriate for situations in which a third party (parent, company) pays for the usage of the consumer (teenager, employee) but does not control that usage, but it neglects situations in which consumers limit usage to less than their usage rates because of a budget constraint or a limit on their willingness to pay more than certain amounts for the service.

Our second model factors in the latter aspect by assuming that each customer has a willingness-to-pay amount or budget constraint w, which is the most it will pay for the service during each period. With x denoting usage rate as in the first model, Model 2 assumes that (w,x) has a joint probability density function over the consuming population, with The probability that a customer chosen at random has is

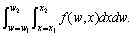
We assume for Model 2 that every potential customer actually subscribes, or, alternatively, that f applies only to subscribing consumers. Assuming that customers are cost minimizers, a customer with parameter pair (w,x) in a period where (a,b) applies will

choose A and pay a to A if or

choose B and pay to B if

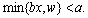
In other words, if either the willingness-to-pay amount w is less than a, or the full-usage per-hit-basis cost bx is less than a, then and only then will the customer subscribe to company B. In this case, then the customer limits its hits to y such that . On the other hand, a customer who and subscribes to A uses its hit rate x but pays only a.

It follows for Model 2 that the average revenues per consumer to A and B for a period in which (a,b) applies are

(3)

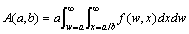
(4)

We assume here that both companies know f and wish to maximize their own revenues by choices of the cost variable under their control.

Dynamic behavior, equilibria, and price wars

As indicated above, companies A and B can change their costs to customers periodically. We will assume this occurs for each period, but no generality would be lost if changes were allowed only sporadically, for example every tenth period. Because each company could gain a competitive advantage if it knew the other company's new fee before it set its own, we will assume that new fees are determined and announced simultaneously. In the absence of collusion, this implies that each company must estimate or guess what the other will charge when it sets its new fee. This casts the price-changing behavior as a repetitive noncooperative game in which the pricing strategies used by the companies could have various forms.

One of these, which we refer to as naive strategies, is for each company to set its new price to maximize its revenue under the assumption that the other company will not change its price in the coming period. Naive strategies are obviously myopic and can result in very different revenues than anticipated when the other does in fact change its fee. More sophisticated strategies arise when the companies anticipate each others' changes. If this is carried to an extreme, the companies can engage a succession of changes and counterchanges "on paper" before finally arriving at their to-be-announced new fees.

In this paper we will not assume explicit forms or methods for new price determination, but will use an analysis of changes and counterchanges to suggest how the companies' fees might evolve over time, or might be affected by sophisticated computation during a single period. Our procedure begins with a fee pair and determines a series of optimal new prices on an alternating basis for the companies under the assumption that the other company retains its "old price" for at least "one more period." Thus, if A goes first, it computes to maximize then B computes to maximize then A computes to maximize B computes to maximize A computes to maximize and so forth. The result is a series

of potential changes and counterchanges. We denote the series by S, or by to note explicitly the initial position.

Among other things, we are interested in the behavior of as n for and gets large. We write if converges to i.e., if for every there is an such that for all And when for a unique that is the same for every initial position we write and say that S converges uniquely to Our experience with a variety of specific assumptions about and P in Model 1 or f in Model 2 indicates that unique convergence usually occurs although other behaviors are possible. We defer consideration of the latter until later and focus for the moment on unique convergence.

Two forms of unique convergence are possible, namely

with and ,

and

.

In the first case, we refer to as a strong equilibrium point, or S.E.P. for short. It typically occurs when

for all ,

for all .

and is the only such point with this property. If the initial position is , which might be determined by the companies at the start, then neither company has an incentive to change its price and we have If then a succession of revenue-maximizing calculations will drive toward .

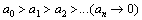
Natural assumptions about and P, or about f, imply that we never have where or when For example, by definition since means that B offers its service without charge, whereas for small positive b. For a similar reason, the second form of unique convergence, never identifies (0,0) as an S.E.P. We refer to as a price war because its typical behavior for with and positive has In this case, each company lowers its price to increase its market share and, hopefully, its revenues, but the long-run outcome is that and are driven toward zero. To avoid such a ruinous result, the companies might revert to pricing schemes that bypass our form of competitive maximization and which could involve covert or overt collusion, perhaps with a revenue-sharing agreement. We will not discuss the legality of such schemes and will focus on non-collusive competitive pricing. However, effects of collusion or `cooperation' will be noted in examples.

We now describe selected results for the two models. Following usual practice, we refer as an equilibrium point if, for all nonnegative (a,b),

1. and .

Assuming differentiability, the first-order conditions for (5) are

and .

The usual second-order conditions for maxima require concavity, i.e, and at but to ensure that (5) holds globally and not just in the vicinity of it may be necessary to look beyond local concavity.

Results for Model 1

When and in (1) and (2) are differentiated with respect to a and b, respectively, we obtain the following first-order conditions for an equilibrium point:

(4A)

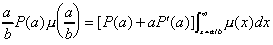
(4B) ,

where If is an equilibrium point, (4A) and (4B) must hold when

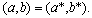
It turns out that there is no (a,b) solution to (4A) and (4B) for many specifications of P and , and in most of these cases we have observed that i.e., a price war. But there are other situations with equilibrium points, and in some of these cases they are strong equilibrium points. We begin with an example of S.E.Ps.

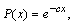
EXAMPLE 1. Our first example assumes that P is a negative exponential function with so that Changes in c allow us to control the effects of the probability that a customer with usage rate x will actually subscribe to the service. For example, if we have when and when

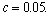
We combine P with the negative power function for with parameters k and defined by

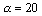
with and The special case of has limited interest because then the expected value of x, defined by is infinite. For , For example, if the average number of hits per customer during one period equals 40.

The first-order conditions (4A) and (4B) for an equilibrium point simplify when we combine the scale parameters c and with the decision variables and define p and q by

.

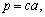
Then (4A) and (4B) reduce to

(5A)

(5B) ,

respectively. It turns out that (5A) and (5B) have a joint positive solution that depends on k when and this solution defines an S.E.P. for each such k with However, when there is no such solution and the situation is a price war with

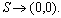
The effect of k for on the a* value at the strong equilibrium point is as follows. As k increases from 2 toward 3, decreases from about 0.3/c to 0, indicating a steady decrease in price at equilibrium as we approach the price war status at At the same time, the revenue ratio at equilibrium favors A slightly but approaches parity as k approaches 3. We note also that both companies' equilibrium revenues approach 0 as Specific calculations show that A's revenue at is 42% of its revenue at at A's revenue is 22% of its revenue at

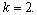
EXAMPLE 2. Our second example involves variations on the price war theme and unusual pricing schemes. We assume throughout that is a negative exponential with parameter

.

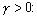
The expected usage rate in this case is

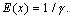
Before we consider particulars, we note a general result for this , namely that if is increasing and concave up to a maximum point and then decreases, we have Many reasonable P functions have the stated properties for, which suggests that the price war situation may well be the rule rather than the exception for instances of Model 1.

Now suppose that, like Example 1, Then satisfies the preceding conditions which ensure that We consider four pricing schemes that avoid a ruinous price war.

1. A chooses a fixed subscription fee and announces that it will not deviate from this fee. We assume that B maximizes its own revenue, given A's announcement. Suppose a is A's fee and is B's best response. Then A chooses a to maximize Computations show that a is approximately (0.7)/c and for is about For example, if and then and or A charges $14 per month and B charges 70 cents per hit. As anticipated, B gets the lions share of the business: the revenue ratio at the solution point is

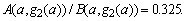
2. B chooses a fixed per-use fee and sticks to it. Then A maximizes its own revenue with best response when B chooses b. We assume that B chooses b to maximize In this case b is approximately and is about (0.5)/c, so when and A charges $10 per month and B charges $2 per hit. The revenue ratio at the solution is

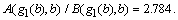
The sum of the companies revenues per potential customer is (0.19)/c for case 1 and (0.25)/c for case 2. Greater totals are possible when A and B collude, to the detriment of consumers. We consider two collusion schemes.

3. The two companies agree to set (a,b) so that their revenues are equal, and do this to maximize what each gets. The (a,b) solution is with

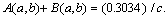
4. The companies collude to maximize which would be the monopolist solution if A and B were the same company. They then agree to split equally. The maximum occurs here when b is effectively and The total revenue, all of which comes from A's fixed fee, is a 21% increase over the total of case 3, and a 94% increase over the total of case 1. When A charges $20 per month in case 4.

We conclude our remarks for Model 1 by considering the unrealistic but analytically interesting situation in which P(x) is constant and positive. In this situation, (4A) and (4B) reduce to

and ,

where When is a negative exponential, as in Example 2, and when is a negative power function (Example 1) with parameters and a succession of price changes and counterchanges drive the other way, toward There are cases in which (4A) and (4B) have a unique solution for example when is a specific convex combination of a negative exponential and a negative power function with In such cases, (a,b) is an equilibrium point if and only with so we have a continuum of equilibrium points. If is not an equilibrium point, a revenue-maximizing change by one company but not the other makes an equilibrium point at which neither company can benefit by a further unilateral change. If both companies change naively and simultaneously in every period, we obtain an alternating pattern in which every other period has and the in-between periods have Finally, because is fixed and when both companies have an incentive to collude and make a and b arbitrarily large.

Results for Model 2

Differentiation of and in (3) and (4) with respect to a and b, respectively, gives the following first-order conditions for an equilibrium point for Model 2:

(6A)

(6B) .

We have examined many instances to Model 2 for specific forms of f, both when w and x are bounded above and when they are unbounded, and found in most cases that (6A) and (6B) have no feasible (a,b) solution. The predominant result in a price war of successive price reductions toward 0.

A main reason for this finding is brought out by considering the separable case in which

,

where g and h are probability density functions for w and x respectively. Separability has the defect that the expected usage rate, given w, is independent of w, whereas we anticipate an increase in that rate as w increases. In other words, it seems likely that consumers who are willing to pay more for the service will, on average, have greater usage rates. We will, however, assume separability in what follows because it simplifies matters and facilitates illustrations of key points.

Given separability, let H and denote the cumulative distribution function and the first derivative of h, respectively. It can then be shown that (6A) and (6B) have no feasible (a,b) solution, hence admit no equilibrium point, if

(12)

for all x in the domain of the usage rate variable. When x is bounded with domain it turns out that (12) holds for most h's that seem reasonable, and it takes some imagination to formulate h's that violate (12) over some subdomain of Even then there is no assurance that (6A) and (6B) have a solution. In fact, we have failed thus far to construct a specific example with f separable and w and x bounded that has an S.E.P.

Plausible failures of (12) are easier to imagine when x is unbounded. We conclude with one such case that has an S.E.P.

EXAMPLE 3. For scaling convenience, we define a separable f by

for all .

Then in the units used for x and w. For example, if each unit of w represents $10, and each unit of x represents 7 hits, then the average willingness to pay is $20 and the mean usage rate, prior to reductions caused by budget constraints, is 14 hits per period. The unit interpretations of $10 for w and 7 hits for x are presumed in what follows.

Our f admits a unique feasible solution for (6A) and (6B) at and the solution is an S.E.P. In `real' terms, A charges $1.50 per month and B charges $1.30 for 7 hits, or about 19 cents per hit, at equilibrium. The average per capita revenues are and , so A has a slight edge over B.

The preceding revenues translate into 38.5 cents per consumer for A and 36.5 cents per consumer for B. These amounts, which seem low in view of the average willingness to pay of $20, are a consequence of competition. For example, if B stopped offering the service, leaving A without a competitor, A would change a from 0.15 to 2, or $20, and realize a 10-fold increase in revenue to $3.85 per consumer on average. In other words, about 19% of the original consumers would pay A the new fee of $20 per month, and the others would stop using the service altogether.

Acknowledgements. We thank Bill Infosino for his comments on an earlier draft of this work.

Notes

This paper was prepared for and presented at a conference in January 1997 organized by the Harvard Information Infrastructure Project. It will appear in the proceedings of that conference, "Internet Publishing and Beyond: The Economics of Digital Information and Intellectual Property," D. Hurley, B. Kahin, and H. Varian, editors, Cambridge, Mass.: MIT Press, 1997.

References

Adams, W. J., and Yellen, J. L. (1976). Commodity bundling and the burden of monopoly. Quart. Journal Economics, 90, 475-498.

Bakos, Y., and Brynjolfsson, E. (1977). Aggregation and disaggregation of information goods: Implications for bundling, site licensing and micropayment systems. In Internet Publishing and Beyond: The Economics of Digital Information and Intellectual Property. D. Hurley, B. Kahin, and H. Varian, eds., MIT Press. To appear. Available at http://www.gsm.uci.edu/~bakos.

Chuang, J. C.-I., and Sirbu, M. A. (1997). Network delivery of information goods: Optimal pricing of articles and subscriptions. In Internet Publishing and Beyond: The Economics of Digital Information and Intellectual Property. D. Hurley, B. Kahin, and H. Varian, eds., MIT Press. To appear. Available at http://www.epp.emu.edu/~chuang.

Cosgrove, J. G., and Linhart, P. B. (1979). Customer choices under local measured telephone service. Public Utilities Fortnightly, Aug. 30, 27-31.

Dyson, E. (1994). Intellectual value, first published in Dec. 1994 in Release 1.0, republished (in an abbreviated form) in Wired, July 1995, and available at

http://www.hotwired.com/wired/3.07/features/dyson.html

Garfinkel, L., and Linhart, P. B. (1979). The transition to local measured telephone service. Public Utilities Fortnightly, Aug. 16, 17-21.

Garfinkel, L., and Linhart, P.B. (1980). The revenue analysis of local measured telephone service. Public Utilities Fortnightly, Oct. 9, 15-21.

Mitchell, B. M., and Vogelsang, I. (1991). Telecommunications Pricing: Theory and Practice. Cambridge Univ. Press.

Odlyzko, A. M. (1996). The bumpy road of electronic commerce, pp. 378-389 in WebNet 96 - World Conf. Web Soc. Proc., H. Maurer, ed., AACE. Available at http://www.research.att.com/~amo.

Odlyzko, A. M. (1997). The economics of electronic journals, to be published. Available at http://www.research.att.com/~amo.

Palmeri, C. (1996). Bully Bell. Forbes, Apr. 22, pp. 92, 94.

Picarille, L. (1996). Licensing lessons. Computerworld, Dec. 9.

Schmalensee, R. (1982). Pricing of product bundles. J. Business, 57, S211-S230. Comments on pp. S231-S246.

Varian, H. R. Pricing information goods. Available at http://www.sims.berkeley.edu/~hal/people/hal/papers.html.

Varian, H. R. Buying, renting and sharing information goods. Available at http://www.sims.berkeley.edu/~hal/people/hal/papers.html.

Wilson, R. (1993). Nonlinear Pricing. Oxford Univ. Press.

The Authors

Peter Fishburn is a principal technical staff member at AT&T Labs - Research. He received his Ph.D. from Case Institute of Technology in 1962, and joined AT&T in 1978 after serving as a research professor of management science at Penn State. His research interests focus on discrete mathematics and decision theory.

E-mail: fish@research.att.com

Andrew Odlyzko is Head of the Mathematics and Cryptography Research Department at AT&T Labs, and also Adjunct Professor in the Faculty of Mathematics at University of Waterloo. His professional interests include computational complexity, cryptography, number theory, combinatorics, coding theory, analysis, and probability theory, as well as electronic publishing and electronic commerce. His home page can be found at http://www.research.att.com/~amo.

E-mail: amo@research.att.com

Ryan Siders is a mathematics graduate student at Princeton University. He wrote his first code in 1985 in a Boca Raton (Florida) public school, and he won the Interservice/Industry Simulation and Training Conference's annual prize for simulations in 1996. His work on this paper was done partially during a summer internship at AT&T Labs - Research in 1996.

E-mail: rcsiders@math.princeton.edu

Copyright © 1997, ƒ ¡ ® s † - m ¤ ñ d @ ¥