
How can the Internet meet the needs of an increasing audience, without degrading service? Will the Internet be accessible to all in the future, and if so how? This paper examines several current hypotheses that provide some descriptions of how the future Internet may or may not work. A pricing system for the Internet may be sufficiently elastic to reduce congestion and allow for distributional equity.
Contents
Introduction
The Internet as a network
Description of the technology and cost structure
Efficient prices for Internet services
The distribution question in the Internet
Feldstein's approach
The safety net approach
Concluding remarks
References
Notes
Introduction
The Internet is the most well-known component of what is nowadays globally recognized as the Information Superhighway Network Infrastructure. It stands for Interconnected networks and is an information distribution system spanning several continents.
Besides being a powerful way of generating a variety of applications, ranging from educational to business activities, and of interconnecting millions of users, the Internet is becoming the basis for the society of the next century: the information society.
As any economic system, the Internet also contributes to the emergence of a wide spectrum of issues concerning the allocation of resources among unlimited uses. It raises questions about convergence of different, and previously distinct industries, like entertainment, computer and communications ; increasing demands; technology shifts; and, regulatory and pricing policies.
This paper, which develops an argument first advanced in Cavalcanti and Nogueira (1996), intends to address the latter of these issues. It is divided into four sections, besides this brief introduction. Section 2 deals with the Internet as a network and describes some of the main technological and costs aspects. Section 3 addresses the isssue of how to efficiently price Internet services. Section 4 introduces the distribution question in the discussion of pricing the Internet, by presenting the Feldstein's approach and then the safety net approach. Finally, section 5 shows the concluding remarks.
The Internet as a network
The Internet is a network of computers of global coverage using a protocol of communication called TCP/IP-Transmission Control/Internet Protocol. TCP/IP provides a common language that enables the interconnection among networks of computers, and allows the use of the package switching technology, the main objective of which is to facilitate the transport of information.The history of the Internet goes back to the late 60's, when the Advanced Reseach Projects Administration (ARPA), a division of the U.S. Defense Department, developed the ARPANET to link together universities and high-tech defense contractors. The TCP/IP technology was developed to provide a standard protocol for ARPANET communications. However, the Internet only became to be known as a powerful computer network in the mid-'80s, when the National Science Foundation-NSF created the NSFNET (a backbone service) in order to provide connectivity to its supercomputer centers, and to provide other general services. The NSFNET adopted the TCP/IP protocol and provided a high-speed backbone for developing Internet (MacKie-Mason and Varian, 1994).
Description of the technology and cost structure
Most of the Internet services are supplied through networks with traffic moving over leased telephone lines. However, there is a distinction in how the lines are used by the Internet and the phone companies. The Internet provides connectionless packet-switching service whereas telephone service is circuit-switched (MacKie-Mason and Varian, 1994).
Phone networks use circuit switching: an end-to-end (point-to-point connections between communication parties) circuit must be set up before the call can begin. A fixed share of network resources is reserved for the call and no other call can use those resources until the original connection is closed.
The Internet uses a technology called "packet-switching". The term "packets" (or frames, or cells) refers to the fact that data stream from a computer is broken up into packets of about 200 bytes (on average), which are then sent out onto the network. This technology is connectionless. This means that there is no end-to-end setup for a session; each packet is independently routed to its destination.
The main advantage of packet-switching is that it permits "statistical multiplexing" on the communication lines.
That is, the packets from many different sources can share a line, allowing for very efficient use of the fixed capacity. With current technology, packets are generally accepted onto the network on a first-come/first-served basis. If the network becomes overload, packets are delayed or discarded ("dropped") (Mackie-Mason and Varian, 1994)[ 1 ]
In terms of costs, it is possible to argue that most of the costs of providing the Internet are more-or-less independent of the level of usage of the networks; that is, most of the costs are fixed. The incremental cost of sending additional packets is essentially zero, if the network is not saturated (Mackie-Mason and Varian, 1994).
However, the most interesting aspect associated with the Internet are their remarkable economies scale and scope (associated with the provision of an increasing variety of services, such as e-mail, gopher, WAIS, FTP, TELNET, WWW, video-conferencing, etc). In the case of the United States, from mid 80's up to 1991 the NSFNET backbone service was the largest single government investment in the NSF-funded program [ 2 ].
The cost to the NSF for transport of information across the network has decreased by two orders of magnitude, falling from approximately $ 10 per megabyte in 1987 to less then $ 1.00 in 1989 [ 3 ]. At the end of 1993, the cost was 13 cents.
These cost reductions occurred gradually over a six-year period. While there were some reductions in the cost of data circuits, the majority of savings resulted from industry equipment vendors incorporating what was learned and developing new faster and more efficient hardware and software technologies.
Despite these large achievements of the Internet as an effective way to move information, however, sometimes it becomes congested, and there is simply too much traffic for the routers (computers that direct packets of information) and lines to handle. The only ways the Internet can deal with congestion, at present, is to drop packets, so that some information must be resent by the application, or to delay traffic, and these solutions impose external social costs.
Mackie-Mason and Varian (1994) have identified this problem as the "classical problem of the commons", and suggested that as long as users have access to unlimited Internet usage (as it is today), they will tend to "overgraze", creating congestion that results in delays and dropped packets for other users.
After examining some recent work on controlling congestion, Mackie-Mason and Varian proposed a system that is based on charging per-packet prices that vary according to the degree of congestion, the details of which can be seen in the next section.
Efficient prices for Internet services
Having described the main technological and cost features of the Internet and highlighted the congestion problem likely to arise as the demand for Internet services grows, we address now the question of how to efficiently price those services. This has turned out to be an important issue given the dramatic increase in the demand for the services and the accompanying problems of congestion.
The price system has been suggested as a means of rationing the access to the services, much in the same way as it does for many other marketed goods and services. The thrust of such an approach is to use price discrimination to sort out the congestion problem by way of the establishment of a "priority service" scheme which relates the consumers' willingness to pay for different types of services to the actual price they pay to have their demand satisfied.
Among the various proposals found in the literature, the one set forth by Mackie-Mason and Varian (1994) has received a great deal of attention and is taken here as the basis of our discussion of pricing the Internet. In what follows, a partial equilibrium approach to a market for Internet services is set up and the scheme advanced by Mackie-Mason and Varian is presented and discussed.
Consider a market for Internet services composed by n identical individuals whose preferences are taken to be represented by the following utility function:
u(qi)
where qi denotes the number of packets demanded by consumer i per unit of time (i = 1,...,n).
We thus can define aggregate demand, Q, as
qi = Q
To model the congestion problem one has to define the current total capacity of the network system and the current level of network utilization. Let K be the current total switching capacity of the Internet network. We then define the total utilization of the network, Y, as the following ratio:
Y = Q/K
The congestion problem arises when aggregate demand (Q) is above the current total capacity of the network (K). In this case, the demand of an additional consumer generates an external cost on the inframarginal consumers in the form of delays experienced in sending packets of information through the network. Consequently, although the service may be used privately, its quality is affected by the level of aggregate demand.
Let D represent this delay cost. As D imposes a disutility on consumers, we rewrite the utility function in the folowing way in order to incorporate that external cost:
u(qi) - D
The decision problem faced by consumer i is
Max u(qi) - D qi The network utility is assumed to seeking to maximize total welfare as given by the sum of all consumers' utilities, that is,
Max u(qi) - nD qi Taking into account that D is a function of Y, the above problem of maximization yields the following first-order condition
u'(qi) - nD'(Y)/K = 0 The expression nD'(Y)/K gives the total delay cost imposed on all consumers due to congestion in the network pipes. An efficient way to deal with this problem is to impose a price (or equivalently, a Pigouvian tax) on consumers equal to the total delay cost so as to internalize the congestion externality. Letting p be such a price, with p = nD'(Y)/K, the maximization problem faced by the individual consumers may be rewritten as
Max u(qi) - D(Y) - pqi The first-order condition for the above problem is
u'(qi) = nD'(Y)/K which guarantees that the individuals choose the optimal level of packet demand, that is, the level that takes into account the congestion cost imposed on third parties.
Suppose now there are m firms in the market offering connection access to the Internet network. As with consumers, it is assumed the existence of a representative firm with total capacity supply of K, the only possible difference between firms being with respect to the delay level offered to consumers. This typical firm carries along its physical connections a total of Q packets and charges a price p for each of them.
In the presence of congestion problems, the price the firm charges is a function of the delay level it contracts with the individual consumers. Therefore, firms may compete against each other in terms of delay levels, with difference across firms signalling product (quality) differentiation. Delay-based price discrimination is thus assumed, with prices being denoted by p(D).
The consumer maximization problem now is
Max u(qi) - D - p(D)qi qi,D
The first-order conditions for a maximum are
u'(qi) = p(D)
and
-p'(D)qi = 1
The first condition says that each consumer will use the network facilities to send packets up tp the point where marginal benefit of sending an extra packet equals the price to be paid for that additional unit. The second condition sets the level of delay for which the consumer is indifferent between sticking to his current access provider and switching to another one.
From the firm's point of view, its maximization problem is
Max p(D(Y))Q - c(K) Q,K where c(K) is the cost of providing capacity K.
The first-order conditions for profit maximization are
-p'(D)D'(Y)Y = p(D)
and
-p'(D)D'(Y)Y2 = c'(K)
The first condition shows that the price charged for packet sent should reflect the value of the additional delay associated with capacity utilization Y. The second condition affirms that the value of the additional delay should be equal to the marginal cost associated with capacity supply K.
Taking into account the fact that the expression -p'(D)qi = 1 in aggregate terms becomes
-p'(D)Q = n
and the dependence of Y on Q and K, we arrive at the following result:
p(D) = nD'(Q/K)/K = c'(K)K/Q
This result means that the optimal price leads to an optimal mix of congestion and delay levels, and to an optimal capacity level. Moreover, as nD'(Q/K)K is equal to u'(qi), marginal benefits to individual consumers are also optimal.
It is thus that the optimal price p is set taking into consideration two factors: the marginal cost of production and the marginal social cost of congestion. If the latter component were not accounted for, individuals would tend to demand a quantity qi above the social optimum.
The above analysis shows that some form of price discrimination in terms of capacity supply and delay cost is possible. Mackie-Mason and Varian (1994) have also developed a rationale for pricing consumers according to their specified needs. Such a schedule would define a "type-of-service" scheme based on different priorities and qualities of service as signalled by the individual consumers. Therefore, individual users may choose the class of service most adequate to their needs (applications).
As an example, those individuals demanding e-mail services could afford to experience some delay in sending their messages during peak periods (and would thus be given a low priority status), while those demanding real-time video services could not afford any delay (and would then be assigned a high priority status). This differentiation would be reflected in the pricing structure, with the first group of consumers paying a price less than that charged to the second group of consumers.
We would then have a set of consumers classified according to the priority/quality level required. An associated set of prices, p, is set in accordance with those levels. Suppose then there exist groups of consumers of type
,

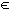
, with f (
) being the frequency distribution function indicating the number of consumers of type
. Each individual of type
may choose from the set of services q and has the following utility function:
u(q, ) - D
with the maximization problem being
Max u(q, ) - D - pq
The solution to this problem gives the demand vectormeaning that efficient prices should reflect the delay cost imposed by the marginal consumer on other individuals.
q(p, )
In aggregate terms we have
Q(p) = q(p, ) f(
) d
The network utility faces the problem of maximizing total welfare:
Max W(p) = [u(q, ) - D - pq(p,
)] f(
) d
Efficient prices for the maximization problem above should be set at
p = u'(q, ) - (D'/K)
The distribution question in the Internet
In the last section we saw how the price system might be used to tackle the congestion problem in the Internet. Frequently, however, the government is concerned with the distributional impact of the pricing policy on the poor. This adds another dimension to the analysis of price determination in the Internet, since the price arrived at while dealing exclusively with the congestion problem might hurt poor consumers if set at too high a level.
In these circumstances, the pricing scheme has to balance conflicting objectives, a problem well known in the economics literature as the trade-off between equity and efficiency.
Some authors (e.g., Mackie-Mason and Varian, 1994) argue that distributional considerations in the Internet should be resolved outside the price system, through, for example, redistributive taxation/subsidization. We here ignore the possibility of resorting to explicit subsidies covered by taxation in order to deal with the equity problem, and instead assume that the trade-off between equity and efficiency is to be resolved by the pricing scheme.
In doing so, we do not mean that the last approach is superior to the first. In this paper we have chosen to explore the problem of distribution within the price system. In other words, we address the case where one is constrained to using prices to deal with the trade-off between equity and efficiency.
Feldstein's approach
One way economists have addressed this question is by following Feldstein's (1972a, 1972b) method of introducing equity considerations in the pricing analysis through the specification of the "distributional characteristic" of a good or service, which is defined as
di=
qi(p,
)
(
)f(
)d
/
qi(p,
)f(
)d
with
being the marginal social utility of income of consumer group
.
The expression for di gives the weighted average of each consumer group's marginal social utility of income, the weight being the participation of each group in the consumption of Internet service i.
Taking the usual assumption that
is inversely related to
, we have that di will be greater for a necessary service than for a luxury service.[ 5 ]
For the special case where the cross-elasticity of demand between two given services i,j is zero, Feldstein's approach yields the following optimal price structure (Feldstein, 1972a):
[(pi - mi)/pi]/[(pj - mj)/pj] = (
jj/
ii)(di/dj)
where
mi,mj = marginal costsThe formula above gives the optimal second-best price when distributional concerns are explicitly taken into account. The trade-off between equity and efficiency is dealt with by the relationship between the efficiency factor (the Ramsey's inverse elasticity rule) and the distributional equity factor (the distributional characteristic ratio).
ii,
jj = own-price elasticities
It seems, however, that Feldstein's method is not the most appropriate to approach the case of Internet services. First, it relies on the distinction between necessities and luxuries, a differentiation not easily applied to the Internet services[ 6 ]. Second, the relationship between the efficiency factor and the distributional equity factor in the Internet is not as straightforward as in the usual analysis of public utilities.
Remember that the main economic problem in the Internet as stressed in the literature was network congestion, that is, when there is too much packet traffic for the transmission system to handle. This highlights the intrinsically shared nature of the Internet's backbones, with several demanders for packet transmission competing for the same resource (bandwidth).
It is the high-end consumers's demand (e.g., for real-time video and audio transmission) that causes the network to get congested, generating a negative externality to low-end consumers (those demanding, e.g., e-mail service).
If one assumes that the demand for high-end services is inelastic to price, while the demand for low-end services is elastic to price, by applying Feldstein's method the former should be more heavily priced than the latter.
However, if the case is, as note 3 above argued, that several institutions, such as public schools and hospitals, which offer public services to a wider spectrum of the population, demand some of the high-end Internet services to fulfil their social objectives, the Feldstein price would hurt them, and indirectly the poor, who relies on those institutions to get access to the Internet services.
The safety net approach
An alternative way to deal with the equity problem in the Internet is the so-called "safety net" approach (Brown and Sibley, 1986). This approach is based on the idea of ensuring that each consumer can consume some minimal level of a given service. It comprises a two-step procedure, by which:
(i) the service(s), the desired level of contribution for consumers and the safety net are set on a social welfare basis;
(ii) the remaining services and consumers are priced according to the efficiency rule.
This approach aims at providing a regulatory safety net for some consumers[ 7 ] at the least cost in terms of efficiency losses.
Formally, this approach objectives to maximize social welfare subject to the safety net constraint. That is to say, given the social goal as expressed by the safety net, it tries to establish a second best price structure that maximizes social welfare at the minimum deadweight loss.
Initially, consider a situation where some Internet service is priced in terms of a flat rate Ao. Due to distributional concerns, the public utility sets a safety net level of consumption and offers an optional pricing scheme in order to handle with the equity issue.
Let qs>0 be the desired level of a certain service i defined by the safety net. An optional two-tariff scheme may be devised so as to make people select themselves on the basis of the chosen tariff. One such a scheme might be the pair (Ai,pi), with
pi = mi
Ai = Ao - miqs
where
Ai = access price to the Internet serviceAo = flat rate
The optional access price Ai<Ao allows more individuals to participate in the market, while the service price pi ensures that quantity demanded is set at efficient levels.
This framework may be used to assess whether there was any repressed demand for the service or not. If any nn>0 new consumers enter the market, then we have a Pareto improvement relatively to the flat rate case as a result of lowering the access price.
Suppose that the individual consuming exactly the safety net quantity level qs has demand curve Ds. The other consumers in the set of consumer types have demand curves posited either above or below Ds. Some type of consumers will be indifferent between the flat rate scheme and the two-tariff scheme, while the ramaining consumers will be either hurt or benefited by switching to the new price structure depending on whether their demand curve lies above or below the demand curve of the indifferent consumer type, respectively.
Therefore, the introduction of a safety net and of a new optional pricing scheme makes those individuals consuming qi < qs better off with no loss of utility for the remaining consumers. A Pareto improvement is thus reached through price self-selection[ 8 ].
In the case of the Internet, we might think of a scheme that defines some basic service i as being socially relevant, the access price of which is set a lower level than the initial situation. We then might achieve a Pareto improvement by having more people having access to that service at a lower access price, while minimizing the cost of doing so by charging a price equal to marginal cost for the quantity consumed.
Concluding remarks
This paper has attempted to give an overview of how the price system can be used in a network environment like the Internet to tackle issues of congestion and distributional equity. The latter question is explicitly introduced in the body of the literature dealing with first best solutions to the congestion problem either by following Feldstein's method or the safety net approach. By comparing these latter two approaches, we reach the conclusion that it may be more adequate to the Internet case to resort to the safety net model than Feldstein's.
The Authors
José Ricardo Nogueira and José Carlos Cavalcanti are members of the faculty in the Department of Economics at the Universidade Federal de Pernambuco-UFPE Cidade Universitaria in Brazil.Department of Economics
Universidade Federal de Pernambuco-UFPE
Cidade Universitária, 50670-901 Recife-Pe Brazil
Phone: (081)271-8381 Fax: (081)271-8378E-mail:
José Ricardo Nogueira jrbn@npd.ufpe.br
José Carlos Cavalcantijcc@di.ufpe.pe
Notes
The authors wish to thank the Administrative Committee of the Internet/Brazil for financial support which permitted their presentation of a previous paper (Cavalcanti and Nogueira, 1996) at the 4th International Conference in Telecommunication Systems, Modelling and Analysis, in Nashville, and at a seminar at the International Computer Science Institute-ICSI, University of California, Berkeley, USA, in March/1996.
1. Recent technical papers for the next generation of IP protocols are adressing a much broad use of Internet connections, such as "one to many" simultaneous connections, and the problems related to new applications like multimedia (text, graphics, images, motion video, sound), as well as a larger number of IP adresses, due to the tremendous growth of the number of hosts within the Internet.
2. From 1991 the American government began to remove subsidies to regional networks and to pave the way for commercial activities.
3. In the same period the speed of data transmission of the NSFNET (bandwidth), evolved from 1.544 Mbps (mega bits per second) to 45 Mbps. For the period of 1995-1999 it is expected that the bandwidth for the Internet in the USA will be between 155 and 1000 Mbps.
4. The additive form of the utility function is taken for the sake of simplicity.
5. This means that the higher the income elasticity of demand for a service, the lower is the di associated with that service.
6. For instance, it is not clear if e-mail service should be considered a necessity and a multimedia service a luxury. It may be that for schools and hospitals the latter should be regarded as a necessity.
7. Defined as a limited group of consumers entitled to preferential treatment.
8. It is possible to demonstrate that for the firm there would be an increase in profit with the introduction of the new price scheme, contributing then for an increase in total surplus (see Brown and Sibley, 1986).
References
S. Brown and D. Sibley, 1986. The Theory of Public Utility Pricing. Cambridge, Eng.: Cambridge University Press.
J. C. Cavalcanti and J. R. Nogueira, 1996. "The Internet, its Brazilian model and an approach to a pricing policy for its operation in Brazil," Annals of the 4th International Conference on Telecommunication Systems, Modeling, and Analysis, Nashville, Tennessee.
M. Feldstein, 1972a. "Distributional equity and the optimal structure of public prices," American Economic Review.
M. Feldstein, 1972b. "Equity and efficiency in public sector pricing: the optimal two-part tariff," Quarterly Journal of Economics.
J. Mackie-Mason and H. Varian, 1995. "Pricing the Internet," In: Public Access to the Internet. Brian Kahin and James Keller (eds.), Cambridge, Mass.: MIT Press, pp. 269-314, and at http://www.spp.umich.edu/spp/papers/jmm/Pricing_the_Internet.ps.Z

Copyright © 1997, ƒ ¡ ® s † - m ¤ ñ d @ ¥